「摩擦力は垂直荷重(抗力)に比例する」というクーロンの摩擦法則は、ダビンチ、アモントンにより研究が行われ、クーロンによる精力的な実験によってまとめられた経験則です。ここでは、なぜ摩擦力が垂直荷重に比例するかについて、真実接触の概念を中心に、ミクロな視点から解説します。
固体の表面
非常に滑らかに見える光沢のある表面にも、表面粗さがあります。機械工学の分野で寸法の標準に使われるブロックゲージという鋼製のブロックがあります。サブミクロンの精度を保証するために、表面粗さは、それよりも小さくする必要があります。図1は、ブロックゲージの表面を拡大したAFM像です。縦軸のスケールは20nm(0.02µm)です。この凸凹の大きさは光の波長よりもずっと小さいので、肉眼では勿論のこと、光学顕微鏡で見ても鏡のようにしか見えません。このことから、高精度に仕上げた金属の板の表面にも凹凸があること、私たちの身の周りにあるほとんど全ての物に表面粗さがあることが容易に想像出来ます。表面粗さのある接触面で、常に摩擦力が発生していることになります。

図1 ブロックゲージの表面粗さを示すAFM*像。高さ方向に拡大している。10nmくらいの細かな凸凹がある。
AFM:atomic force microscope の略。縫い針の先端よりも1000倍以上鋭い針を使って表面をなぞることで、表面形状をナノメートル以下の分解能で測定出来る計測装置。
摩擦力が働く原子同士の距離
表面粗があると、向かい合う面の全てが接触することはなく、表面間の距離は一定にはなりません。例えばブロックゲージのような、十分に平滑な表面同士が接触する場合でも、全面が接触していないことは容易に想像出来ます。では、図2のような形で接触しているとき、摩擦力はどの部分に作用しているのでしょうか?
すき間のある部分には当然ながら力は作用しません。摩擦力は原子同士が接触している部分に作用します。その距離は、だいたい結晶の原子間隔ほどの距離(〜1Å)になり、この面積は、固体表面が弾性変形や塑性変形を生じつつ、荷重を支えている面積に相当します。
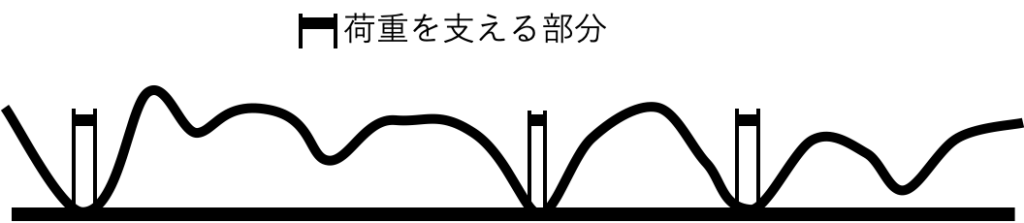
図2 表面粗さのある表が接触している様子(分かり易くするために、一方は平坦面にしています)。摩擦力が作用するのは、荷重をを支えている部分であり、そこでの原子間の距離は、斥力を受ける程度の距離まで接近している。
摩擦力が荷重に比例する理由
摩擦力が作用する面積は、「真実接触面積」と呼ばれています。この真実接触面積が荷重を支えます。図3は、比較的きれいな金属表面のイメージです。丁寧に洗浄しても、その辺に置いておくと、数分か数時間で表面は薄い油に覆われてしまいます。油に覆われていなくても、金属表面は酸化しており、その上には気体分子や水が吸着しています。このような部分が真実接触面となって荷重を支え、そこで摩擦力が発生します(図4)。摩擦力の作用は、油同士が接触する場合、水が挟まれて接触する場合、酸化した金属原子が弾性接触する場合、酸化膜を破って金属が接触する場合など、どのような接触状態でも原子同士が斥力を受ける距離まで近づいた時に生じます。その相互作用の強さは、油同士がが接触するときと、金属同士が接触する時で異なります。しかし、金属表面にある無数の突起の接触を考えたとき、汚れ具合も、酸化の度合いも、材料の硬さも、全て同様なので、どこの突起が接触しても、多様な接触状態が同じような割合で含まれていることになります。
以上より、接触させる物(表面)の組合わせが同じならば、「真実接触面積に比例した摩擦力が作用する」と考えることができます。クーロンの摩擦法則で、摩擦力Fが荷重Lに比例する、即ちF=µL(µは摩擦係数)となることの説明では、この真実接触面積の考え方がベースになっています。またこのことから、別の材料を組合わせたり、表面の汚れ具合が異なる条件では、比例の関係は維持されながらも、摩擦係数が変化することも説明できます。

図3 比較的きれいな金属表面のイメージ。金属表面は酸化し、酸素原子は深く侵入し金属原子の配列を乱す。表面には物理吸着した酸素や水の分子、そのうち一部は乖離して金属と反応している。また、空中にはわずかに油(炭化水素)が浮遊し、表面に吸着している。
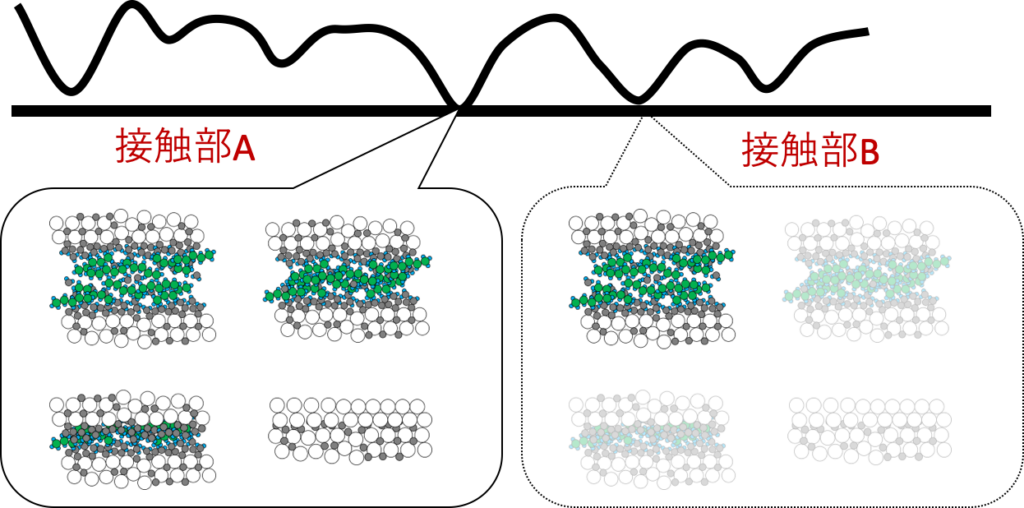
図4 比較的きれいな金属表面が接触している様子。接触部Aでは、部分的に塑性変形していて、圧力の高い部分では金属同士の接触が生じているが、水分子や酸素分子を介して接触している部分もある。接触部Bは、わずかに接触し始めたところだが、荷重が増えれば接触部Aと同様になる。同じ面であれば、どの点で接触しても、金属や吸着分子は同じような状態で接触する。即ち、真実接触面には、単位面積当たり等しい摩擦力が作用する。
真実接触面積
この真実接触面積の大きさはどの程度の大きさになるのでしょうか? 重さ10kgの金のブロックが、硬い平面に置かれている状態を考えます。金の表面粗さの突起が塑性変形して、その面積だけで重さを支えていると仮定すると、金の硬さ25 kg/mm2を用いて、次式から真実接触面積SRを計算することができます。
SR = 10(kg)/25(kg/mm2)
この式から、真実接触面積は、0.4 mm2になります。金のブロックが立方体の場合は、底面の大きさ(見かけの接触面積)は、6360 mm2になるので、見かけの接触面積の0.006%しか接触していないことになります。実際には、弾性変形している部分でも荷重を支えているので、真実接触面積はもっと大きくなるはずですが、仮に100倍になったとしても、0.6%に留まります。もしかすると、真実接触面積はさらに大きいかも知れませんが、極端に大きくなることは無いと考えられます。なぜならば、仮に自重での真実接触面積が、見かけの接触面積の20%だとすると、荷重を5倍にしただけで真実接触面積は100%となり、それ以上摩擦力が増えないことになります。荷重を5倍まで増やさなくても、表面粗さの凹みの部分は荷重を増やしたときに容易に接触しないので、摩擦力が荷重に比例することが難しいでしょう。したがって、摩擦力が荷重に比例するためには、真実接触面積の大きさが、見かけの接触面積に比べて十分に小さいことがカギとなっています。

図5 真実接触面積と見かけの接触面積の大きさの比較。粗さのある80mm角(10kg)の金のブロックを平滑面に置いたとき、塑性変形だけを仮定すると、真実接触面積の大きさは0.4 mm2になる。見かけの接触面積と比較すると、その面積の0.006%でかなり小さい。
真実接触面積を正確に測定する方法
結論から言うと、真実接触面積の大きさを直接測定する方法はありません。例えば、ガラスに金属を接触させ、ガラス面から金属を観察する場合は、光の波長の制限を受けるため、レーザー光を使ってもナノメータの分解能を得ることも困難です(原子の大きさは可視光の波長よりも2桁以上小さくなります)。光の波長を短くしていくと(x線になると)、金属表面での反射が無くなりますし、電子線では、可視光に対するガラスのように都合の良い材料がありません。電気抵抗から求めることも考えられますが、縮流抵抗やトンネル電流、表面酸化膜などの影響があり、抵抗値が求められたとしても、その結果の扱いが困難です。接触した状態のまま固定して、断面を薄くスライスしてTEM(透過型電子顕微鏡)で観察する方法が報告されています。この方法ならば、真実接触面積を正しく見積もれる可能性がありますが、断面ということで限界があります。
摩擦力が作用する距離に関する補足説明
金属表面同士が滑っている間に、表面間の距離が原子スケールで見ても不変ならば(相互作用エネルギーが一定であれば)、摩擦力は発生しません。しかし、個々の原子の動きを考えると、お互いを乗り越えながら進むため原子間隔はわずかに変化します(図6)。このとき、斥力領域の相互作用エネルギーの変化は急峻なので、エネルギーは大きく変化します。その結果、この大きく変動したエネルギーの一部が散逸し、摩擦力が発生します。
上に述べた「摩擦力が働く原子同士の距離」の説明では、すき間には力が働かないとしましたが、実際には引力が作用しています。この引力によって、摩擦力は働かないのでしょうか? 原子同士の乗り越えが生じたときに、厳密に言えば引力領域にある原子同士の間隔も変化します。しかし、引力領域のポテンシャル勾配が、斥力領域よりも極端に小さいため、引力が摩擦力に与える影響は限りなく小さくなります。
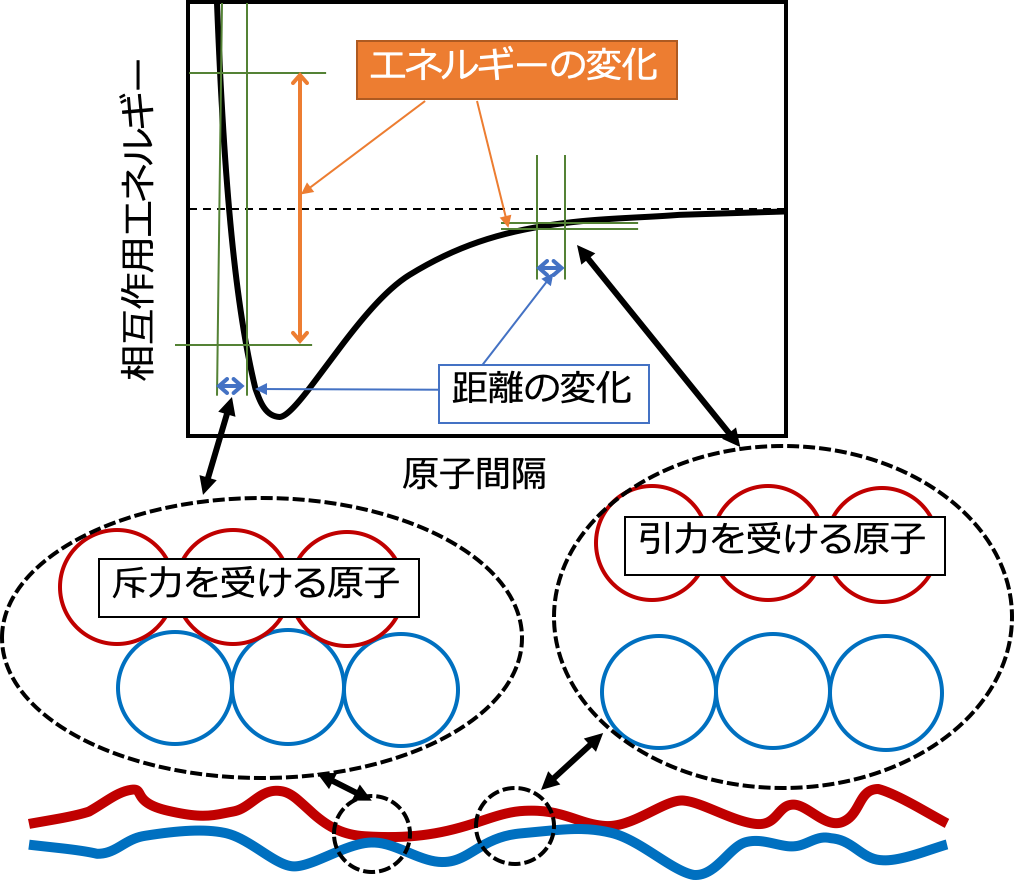
図6 赤い金属表面と青い金属表面が接触し、滑る時、それぞれの原子間距離の変化とそのときに生じる相互作用エネルギー変化。斥力を受ける原子が相手の原子を乗り越える時に垂直方向の距離が変化する。この時の変位に対して、斥力領域では大きなエネルギー変化が生じるのに対し、引力領域で生じるエネルギー変化は僅少になる。
